Why does Deep Learning work?
This is the big question on everyone’s mind these days. C’mon we all know the answer already:
“the long-term behavior of certain neural network models are governed by the statistical mechanism of infinite-range Ising spin-glass Hamiltonians” [1] In other words,
Multilayer Neural Networks are just Spin Glasses? Right?
This is kinda true–depending on what you mean by a spin glass.
In a recent paper by LeCun, he attempts to extend our understanding of training neural networks by studying the SGD approach to solving the multilayer Neural Network optimization problem [1]. Furthermore, he claims
None of these works however make the attempt to explain the paradigm of optimizing the highly non-convex neural network objective function through the prism of spin-glass theory and thus in this respect our approach is very novel. And, again, this is kinda true
But here’s the thing…we already have a good idea of what the Energy Landscape of multiscale spin glass models* look like–from early theoretical protein folding work by Peter Wolynes to modern work by Ken Dill, etc [2,3,4]). In fact, here is a typical surface:
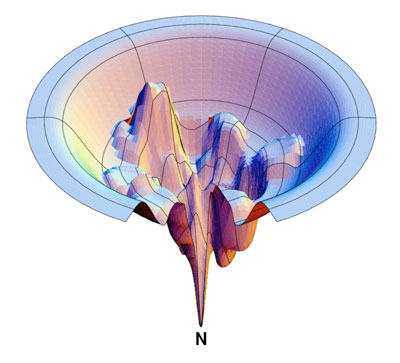
https://news.stonybrook.edu/wp-content/uploads/2018/07/dilldiagram.jpg
Let us consider the nodes, which above represent partially folded states, as nodes in a multiscale spin glass–or , say, a multilayer neural network. Immediately we see the analogy and the appearance of the ‘Energy funnel’ In fact, researchers have studied these ‘folding funnels’ of spin glass models over 20 years ago [2,3,4]. And we knew then that
as we increase the network size, the funnel gets sharper
Note: the Wolynes protein-folding spin-glass model is significantly different from the p-spin Hopfield model that LeCun discusses because it contains multi-scale, multi-spin interactions. These details matter.

Spin glasses and spin funnels are quite different. Spin glasses are highly non-convex with lots of local minima, saddle points, etc. Spin funnels, however, are designed to find the spin glass of minimal-frustration, and have a convex, funnel shaped, energy landscape.
This seemed to be necessary to resolve one of the great mysteries of protein folding: Levinthal’s paradox [5]. If nature just used statistical sampling to fold a protein, it would take longer than the ‘known’ lifetime of the Universe. It is why Machine Learning is not just statistics.
Deep Learning Networks are (probably) Spin Funnels
So with a surface like this, it is not so surprising that an SGD method might be able to find the Energy minima (called the Native State in protein folding theory). We just need to jump around until we reach the top of the funnel, and then it is a straight shot down. This, in fact, defines a so-called ‘folding funnel’ [4]
So is not surprising at all that SGD may work.
Recent research at Google and Stanford confirms that the Deep Learning Energy Landscapes appear to be roughly convex [6], as does LeCuns work on spin glasses.
Note that a real theory of protein folding, which would actually be able to fold a protein correctly (i.e. Freed’s approach [7]), would be a lot more detailed than a simple spin glass model. Likewise, real Deep Learning systems are going to have a lot more engineering details–to avoid overtraining (Dropout, Pooling, Momentum) than a theoretical spin funnel.
[Indeed, what is unclear is what happens at the bottom of the funnel. Does the system exhibit a spin glass transition (with full blown Replica Symmetry Breaking, as LeCun suggests), or is the optimal solution more like a simple native state defined by but a few low-energy configurations ? Do DL systems display a phase transition, and is it first order like protein folding? We will address these details in a future post.] In any case case,
It is not that Deep Learning is non-convex–is that we need to avoid over-training
And it seems modern systems can do this using a few simple tricks, like Rectified Linear Units, Dropout, etc.
Hopefully we can learn something using the techniques developed to study the energy landscape of multi-scale spin glass/ spin funnels models. [8,9], thereby utilizing methods theoretical chemistry and condensed matter physics.
In a future post, we will look in detail at the folding funnel including details such as misfolding, the spin glass transition in the funnel, and the relationship to symmetry breaking, overtraining, and LeCun’s very recent analysis. These are non-trivial issues.
I believe this is the first conjecture that Supervised Deep Learning is related to a Spin Funnel. In the next post, I will examine the relationship between Unsupervised Deep Learning and the Variational Renormalization Group [10].
I discuss more of this on my YouTube channel : MMDS 2016 Talk
Update: Jan 2018
We have observed what I conjectured 3 years ago on my blog and at MMDS 2016 –the Spin Glass of Minimal Frustration (left) appearing in Deep Networks (right). Stay tuned for some very exciting results into theory of Deep Learning.
Update: Sep 2018: Predictions can come true
This paper was just brought to my attention on “VISUALIZING THE LOSS LANDSCAPE OF NEURAL NETS” which exactly verifies the above predictions…3 years later
• “We observe that, when networks become sufficiently deep, neural loss landscapes quickly transition from being nearly convex to being highly chaotic. This transition from convex to chaotic behavior coincides with a dramatic drop in generalization error, and ultimately to a lack of trainability.”
• “We show that skip connections promote flat minimizers and prevent the transition to chaotic behavior, which helps explain why skip connections are necessary for training extremely deep networks”
Update: October 2018
3 Years after posting this blog, I have formalized the ideas into a new theory of learning. The first of the papers has been published
Update: September 2019
As predicted, visualizations of ResNet25 show exactly this result

Learn more about us at: http://calculationconsulting.com
[1] LeCun et. al., The Loss Surfaces of Multilayer Networks, 2015
[2] Spin glasses and the statistical mechanics of protein folding, PNAS, 1987
[3] THEORY OF PROTEIN FOLDING: The Energy Landscape Perspective, Annu. Rev. Phys. Chem. 1997
[4] ENERGY LANDSCAPES, SUPERGRAPHS, AND “FOLDING FUNNELS” IN SPIN SYSTEMS, 1999
[5] From Levinthal to pathways to funnels, Nature, 1997
[6] QUALITATIVELY CHARACTERIZING NEURAL NETWORK OPTIMIZATION PROBLEMS, Google Research (2015)
[7] Mimicking the folding pathway to improve homology-free protein structure prediction, 2008
[8] Funnels in Energy Landscapes, 2007
[9] Landscape Statistics of the Low Autocorrelated Binary String Problem, 2007
[10] A Common Logic to Seeing Cats and Cosmos, 2014


Reblogged this on AOS.
LikeLike
Very interesting post !
For a newbie DL user, as a cond-mat physicist, I can only agree with your short essay. It seems intuitively that DL and SG networks are intimately related. Dropout makes me think, perhaps wrongly, about another kind of randomness than frustration (with different effects): impurities. In any event, a great field of research with still many more promising applications.
Thanks a lot. Cheers
LikeLiked by 1 person
Really nice topic! Thanks!
LikeLike
Another consequence of energy funnels with global minima is the existence of “alternative truths” — several stable configurations of the same physical model. In the structural biology world, such configurations can manifest as alternative binding modes of a ligand to a receptor, as shown here https://www.ncbi.nlm.nih.gov/pubmed/18058908 (I’m the first author). Another plausible example of the alternative configurations is the existence of different stable protein configurations, such as in the case of prion diseases.
I wonder what local minima of a deep learning network can stand for.
LikeLiked by 1 person
Thanks a lot. I have enjoyed this bright piece by traveling back in time. Found the images very much useful to have a richer envision of the impact that some astronomy works had in all the sciences. And vice versa..
LikeLike